¿Por dónde empezar la tabla de verdad?

Siempre que empecemos a hacer una tabla de verdad lo debemos hacer en el orden que se propone a continuación y tomando en cuenta las siguientes recomendaciones:

1. Iniciar de izquierda a derecha y de la parte interna hacia la externa.


2. Obtener primero el valor de las proposiciones simples (p, q, r, s, t, etcétera).


3. Obtener el valor de las conectivas dentro de los paréntesis a partir del valor de las conectivas simples involucradas. Recuerda siempre ir de izquierda a derecha. Si tuviéramos el siguiente caso:

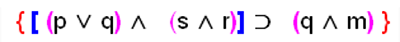
Tendríamos que realizar el primer paréntesis, luego el segundo, después obtener el valor de la conectiva principal dentro del corchete que en este caso es una conjunción y sólo después podremos continuar con el paréntesis a la derecha del corchete.

4. A continuación, obtener el valor de la conectiva principal dentro del corchete, a partir del valor de las proposiciones que la componen.


5. Después obtener el valor de la conectiva principal dentro de la llave, a partir del valor de las proposiciones que la componen.


6. Siempre que existan proposiciones simples a las que les anteceda una negación, será necesario obtener su valor y después negarlo. Por ejemplo, en los casos que aparecen a continuación, primero habría que obtener el valor de la proposición simple que se encuentra a la derecha de la negación y después negar esos valores.



7. Si tenemos el caso de que una proposición compuesta dentro de un paréntesis sea llave o corchete y que está afectada por una negación, primero habrá que obtener el valor de la conectiva principal dentro del signo de agrupación y después a ese valor aplicarle la negación. Por ejemplo:

1. 
   En este caso tendría que obtener el valor de la conjunción y posteriormente negar esos valores.


2. 
   En este caso tendría que obtener primero el valor de la disyunción y el condicional por separado, posteriormente, el valor de la conjunción y finalmente negar los valores de esta última conectiva.


3. 
   En este caso tendría que obtener primero el valor del condicional y la conjunción por separado, después el del bicondicional, a continuación el de la conjunción y finalmente negar el valor de esta última.


4. 
   En este caso observo que la negación afecta al corchete, así dentro de éste, debo obtener el valor de la conjunción dentro del corchete y el valor de “s” por separado, luego el del bicondicional y negar posteriormente los valores de esta última conectiva, pues la negación niega el valor del bicondicional que es la conectiva principal dentro del corchete.


5. 
   En este caso, cada negación afecta a la conectiva principal dentro del corchete en cada caso, así, primero tendría que obtener el valor de la conectiva dentro del paréntesis, posteriormente, el valor de la conectiva principal dentro de la llave que, en el primer caso es la conjunción y en el segundo es el bicondicional, finalmente tendría que negar los valores de cada una por separado. La tabla concluiría obteniendo los valores del condicional a partir de los valores de la negación de lo que se encuentra dentro del corchete.

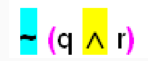
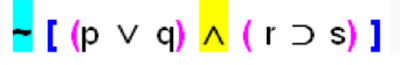
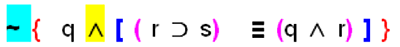
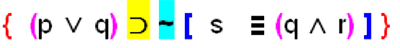
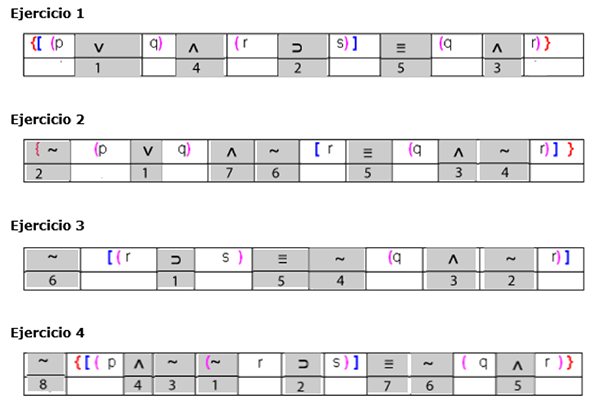
A manera de resumen veamos las siguientes proposiciones compuestas donde hemos ordenado numéricamente las conectivas según el criterio de agrupación, es decir, colocamos el 1 en la conectiva que debo obtener primero su valor de verdad, el último número será la conectiva principal.

Explicación de tabla de verdad. La resolución

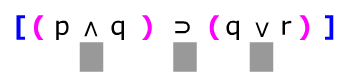
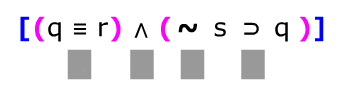
Para resolver una tabla necesitas una fórmula.

2: Falso y verdadero. Siempre será 2

n: Número de variables o letras distintas en la simbolización

Tabla de verdad de las proposiciones compuestas

Pongamos por ejemplo la siguiente proposición ya simbolizada:

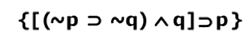
Dibujo la tabla de verdad para saber cuántas posibles combinaciones de verdad y falsedad hay y aplico la fórmula:

Observo que tengo dos proposiciones simples (p y q), por lo tanto sustituyo la “n” por dicho número:

Así, obtengo la siguiente tabla:

Realizo la tabla:

Como habíamos señalado antes, siempre unimos pares de proposiciones para ir haciendo las combinaciones de valores de verdad (le colocaremos el número 1 y 2 para que te sea más claro comprender la explicación) y empezamos desde la parte más interna hacia la más externa. Así, iremos en este orden:

Primero, comenzaremos con la parte que hemos resaltado en azul y que está dentro del paréntesis (  ), e ignoraremos el resto de la proposición.

Podemos notar que el signo dominante dentro del paréntesis es el condicional, y que cada una de las proposiciones simples que lo componen (en este caso p y q) están afectadas por una negación.

Para poder obtener el valor de verdad del condicional, es necesario realizar las negaciones antes, por lo cual empezaremos por ellas (siempre que tengamos proposiciones simples a las que les anteceda una negación, será necesario realizar ésta primero).

Sabemos que el valor de una proposición cambia a su valor contrario al negarse. Así, cuando p es verdadera, su negación es falsa, y viceversa: cuando p es falsa, su negación es verdadera. Así, tenemos:

Es importante destacar que los valores de verdad se colocan debajo de la conectiva que se está realizando, pues si estos valores estuvieran debajo del símbolo del condicional, estaríamos diciendo que corresponden a él. Por ejemplo, si colocáramos los valores de la negación de p debajo de p diríamos que es el valor de p sola sin la negación, etc.

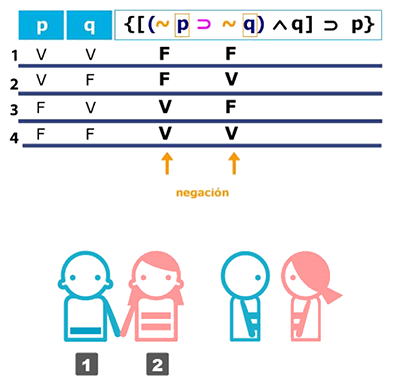
Una vez que hemos realizado las negaciones podemos obtener el valor de verdad del condicional. Sabemos que sólo hay un caso de falsedad del condicional, que es cuando tenemos el antecedente verdadero y el consecuente falso.

Al terminar esta parte de la proposición, hagamos de cuenta que ésta se ha fusionado y se ha convertido en una nueva, la cual debemos considerar como un solo bloque para unirla con la otra que se encuentra dentro de los corchetes [  ].

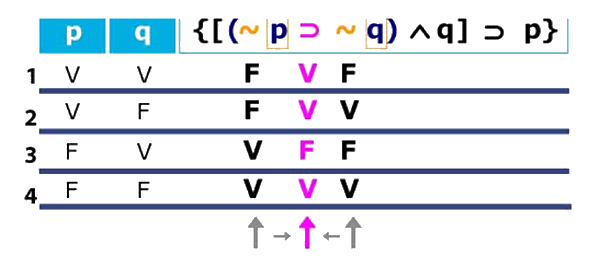
Ya tenemos el valor de la proposición condicional que se encuentra dentro del paréntesis. Ahora la tenemos que unir con la otra parte que es la q. Ya conocemos el valor de q (lo tenemos en las columnas del lado izquierdo). Dado que no está afectada por ninguna negación, simplemente copiamos esos valores:

Ahora podemos obtener el valor de la conectiva principal dentro del corchete. Recuerda que la conectiva principal es siempre la que se encuentra más hacia el exterior de la proposición que estamos considerando, que en este caso es la conjunción.

Sabemos que una conjunción sólo es verdadera cuando sus dos miembros son verdaderos. Cualquier otra combinación de valores de verdad es falsa.

Ya que hemos realizado la combinación de valores de esta proposición al igual que en la anterior, ésta quedará superada y a su vez se convertirá en una nueva, la cual debemos considerar como un solo bloque para unirla con la otra que se encuentra dentro de las llaves  {  }.

Notamos que la conectiva principal dentro de la llave es el condicional, ya que es la que se encuentra más hacia el exterior del bloque que consideramos. Observamos que p es nuestra otra proposición. Ya conocemos su valor, pues lo tenemos en la primera columna de la izquierda, así que copiamos los valores. De esta forma  tenemos:

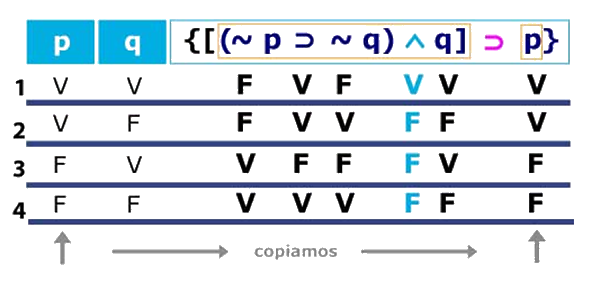
Ahora podemos proceder a realizar el condicional. Sabemos que el único caso de falsedad del condicional es cuando tenemos el antecedente verdadero y el consecuente falso.

El valor que consideraremos dentro del corchete será el que corresponde a la conectiva principal del mismo y que fue el de la columna última que obtuvimos, es decir, el de la conjunción.  A éste lo combinaremos con el de p (que se encuentra a la derecha del condicional).

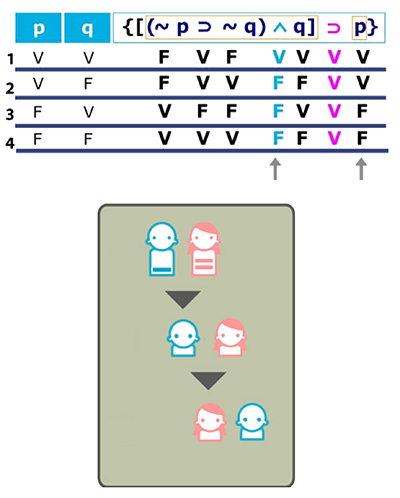
Y… ¡Por fin hemos terminado nuestra tabla!

A modo de resumen, numeraremos los pasos que se han seguido para realizar la tabla de verdad de la proposición:

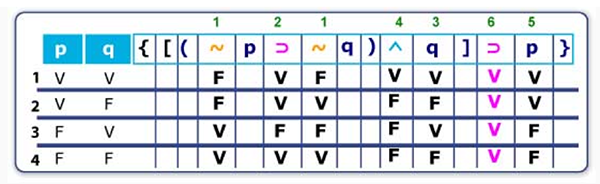
Aparentemente es un proceso difícil, pero en realidad no lo es, solo es cuestión de práctica, por lo cual ahora te tendrás que ejercitar en ello realizando los siguientes ejercicios no sin antes revisar el siguiente video, en él encontrarás un ejemplo sobre la manera de desarrollar una tabla de verdad con proposiciones compuestas:

Bien, ahora realiza los siguientes ejercicios.  Cuando tengas dudas vuelve a revisar la explicación anterior y el video, seguro que lograrás dominar el tema.

Ejercicio

Antes de hacer los siguientes ejercicios, vuelve a revisar todo el procedimiento explicado anteriormente. Te recomendamos tener un formulario con los valores de verdad de las tablas de cada conectiva. Cuando tengas dudas retorna a la explicación anterior.

Realiza la tabla de verdad de las siguientes proposiciones. Una vez que termines, da clic en comparar.

Como último punto es muy importante practicar las tablas de verdad para aprenderlas correctamente. Es por ello que hemos diseñado la siguiente Autoevaluación que te ayudará con tal propósito.

Autoevaluación

Tablas de verdad

Descarga el archivo dando clic aquí para realizar los ejercicios que en éste se te presentan.
descriptionDocumento
Verifica que realizas tu actividad correctamente dando clic aquí.
descriptionDocumento